V-Lab @ ANDC

Trapezoidal method for definite integral

Aim

To Perform Numerical Integration using Trapezoidal Formula for a given data set / function

Theory

What is Trapezoidal rule ?

In mathematics, the trapezoidal rule, also known as the trapezoid rule or trapezium rule is a technique for approximating the definite integral in numerical analysis. The trapezoidal rule is an integration rule used to calculate the area under a curve by dividing the curve into small trapezoids. The summation of all the areas of the small trapezoids will give the area under the curve. Let us understand the trapezoidal rule formula and its proof using examples in the upcoming sections.
The trapezoidal rule is applied to solve the definite integral of the form b∫a f(x) dx, by approximating the region under the graph of the function f(x) as a trapezoid and calculating its area. Under the trapezoidal rule, we evaluate the area under a curve is by dividing the total area into little trapezoids rather than rectangles.

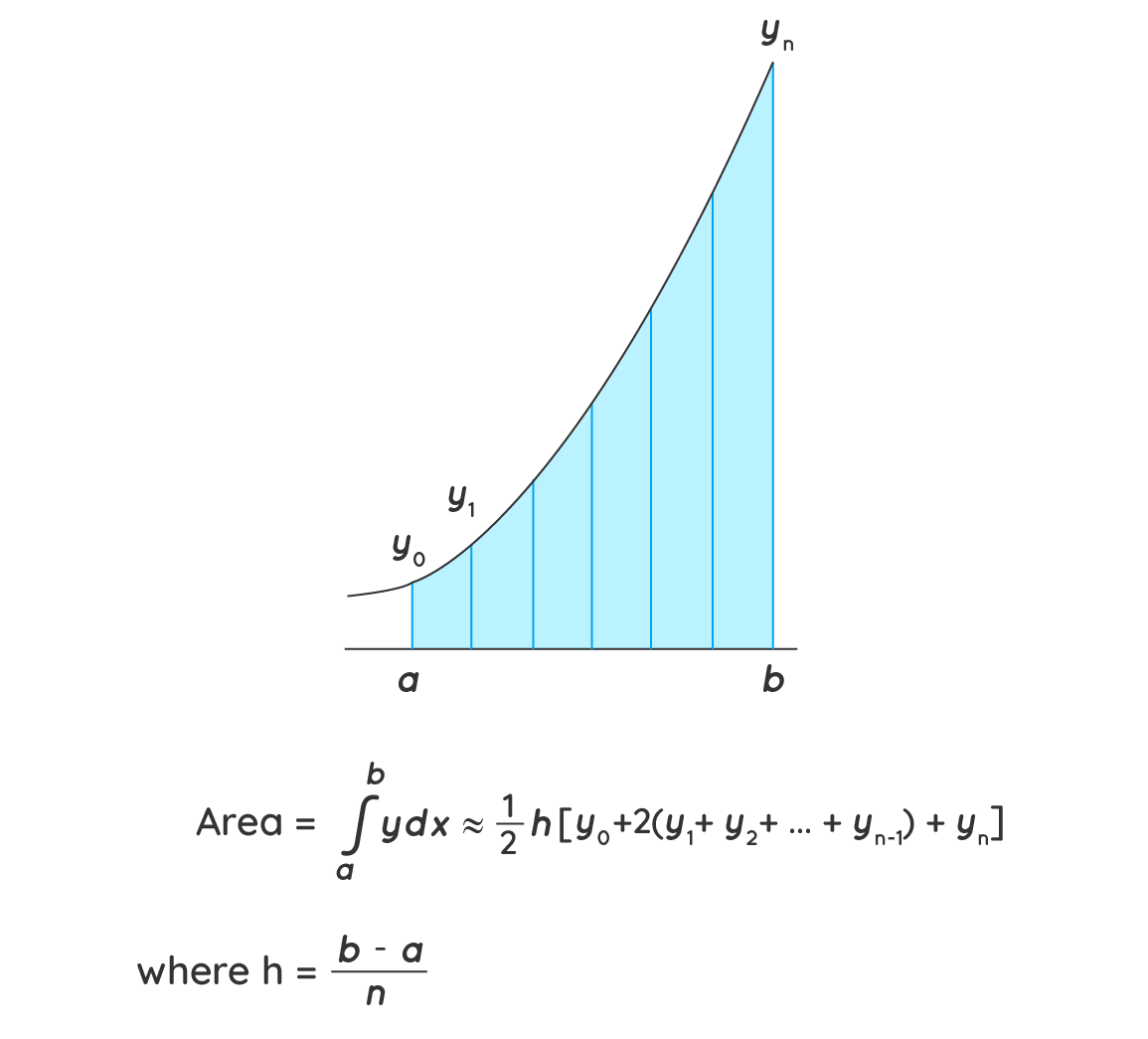
Derivation of Trapezoidal Rule Formula:

We can calculate the value of a definite integral by using trapezoids to divide the area under the curve for the given function.

Let f(x) be a continuous function on the interval (a, b). Now divide the intervals (a, b) into n equal sub-intervals with each of width,

Δx = (b - a)/n, such that a = x0 < x1 < x2 < x3 <…..< xn=b

Then the Trapezoidal Rule formula for area approximating the definite integral b∫af(x)dx is given by:

b∫af(x) dx ≈ Tn = △x/2 [f(x0) + 2f(x1) + 2f(x2) +….2f(xn-1) + f(xn)]

where, xi = a + i△x

If n → ∞, R.H.S of the expression approaches the definite integral b∫a f(x)dx

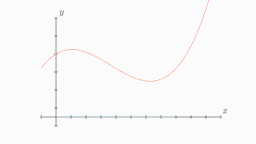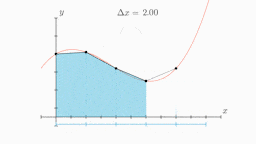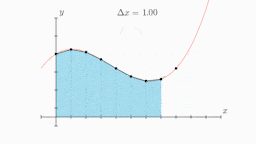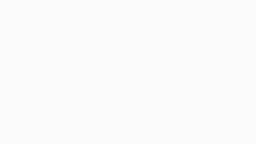
To prove the trapezoidal rule, consider a curve as shown in the figure above and divide the area under that curve into trapezoids. We see that the first trapezoid has a height Δx and parallel bases of length y0 or f(x0) and y1 or f1. Thus, the area of the first trapezoid in the above figure can be given as,

(1/2) Δx [f(x0) + f(x1)]

The areas of the remaining trapezoids are (1/2)Δx [f(x1) + f(x2)], (1/2)Δx [f(x2) + f(x3)], and so on.

Consequently,

∫ba f(x) dx ≈ (1/2)Δx (f(x0)+f(x1) ) + (1/2)Δx (f(x1)+f(x2) ) + (1/2)Δx (f(x2)+f(x3) ) + … + (1/2)Δx (f(n-1) + f(xn) )

After taking out a common factor of (1/2)Δx and combining like terms, we have,

∫ba f(x) dx≈ (Δx/2) (f(x0)+2 f(x1)+2 f(x2)+2 f(x3)+ ... +2f(n-1) + f(xn) )

Procedure

  1. Define function f(x)
  2. Enter initial limit (a), final limit (b), interval (i)
  3. Calculate step size (h)
  4. Using for loop calculate:
    for i= 1:n-1
    k= a+ i*h
    sum+=2*f(x)
  5. sum= f(a)+f(b)
  6. ans= h/2 * sum
  7. Display the answer

Python Code

                        
                            a= float(input("Enter the lower limit: "))
b= float(input("Enter the upper limit: "))
n= int(input("Enter the length: "))

def f(x):
    return (1/(1+x**2))

def trapezoidal(a,b,n):
    h= (b-a)/n
    sum1= f(a)+f(b)

    for i in range(1,n):
        w= a + i*h
        sum1+= 2*f(w)

    total= sum1 * h/2
    return total

result= trapezoidal(a,b,n)
print("Result by Trapezoidal method is: ",result)

Observations

Take Observations from the method and tabulate it for the given intervals.

Plot a graph also. (Interval vs Value).

Result

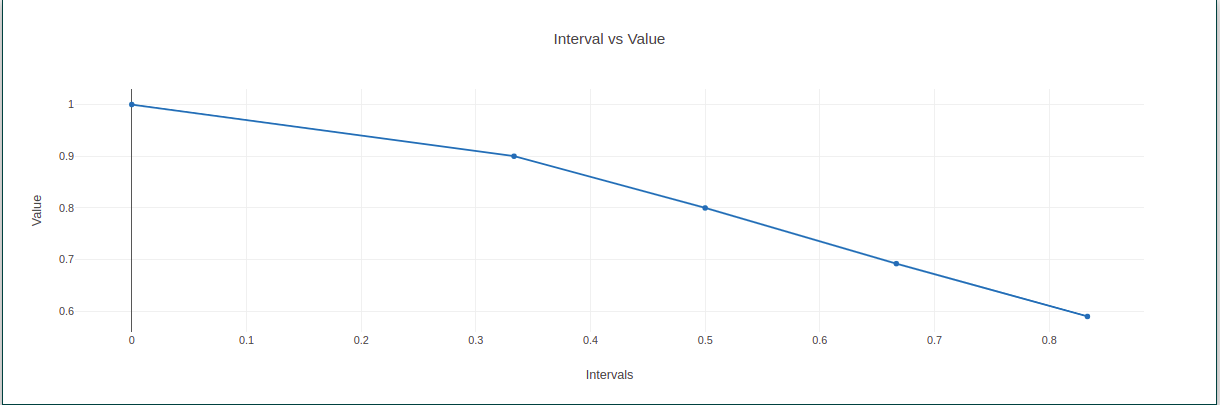
Hence we calculate the definite integral
The summation of all the areas of the small trapezoids will give the area under the curve.

References

Trapezoidal method Byju's

Trapezoidal method Wikipedia