V-Lab @ ANDC

Simpson 1/3 method for definite integral

Aim

To Perform Numerical Integration using Simpson 1/3 Formula for a given data set / function

Theory

What is Simpson 1/3 rule ?

Simpson's rule is one of the numerical methods which is used to evaluate the definite integral. Usually, to find the definite integral, we use the fundamental theorem of calculus, where we have to apply the antiderivative techniques of integration. However, sometimes, it isn't easy to find the antiderivative of an integral, like in Scientific Experiments, where the function has to be determined from the observed readings. Therefore, numerical methods are used to approximate the integral in such conditions. Other numerical methods used are trapezoidal rule, midpoint rule, left or right approximation using Riemann sums. Here, we will discuss Simpson's rule formula, 1/3 rule, 3/8 rule and examples.

Simpson's rule formula:

Simpson's rule methods are more accurate than the other numerical approximations and its formula for n+1 equally spaced subdivision is given by;

b∫a f(x) dx ≈ Sn= Δx/3[f(x0)+4f(x1)+2f(x2)+4f(x3)+....+2f(xn-2)+4f(xn-1)+f(x)]
Where n is the even number, △x = (b - a)/n and xi = a + i△x
If we have f(x) = y, which is equally spaced between [a, b] and if a = x0, x1 = x0 + h, x2 = x0 + 2h …., xn = x0 + nh, where h is the difference between the terms. Or we can say that y0 = f(x0), y1 = f(x1), y2 = f(x2),……,yn = f(xn) are the analogous values of y with each value of x.

Simpson's 1/3rd rule is an extension of the trapezoidal rule in which the integrand is approximated by a second-order polynomial. Simpson rule can be derived from the various way using Newton's divided difference polynomial, Lagrange polynomial and the method of coefficients. Simpson's 1/3 rule is defined by: 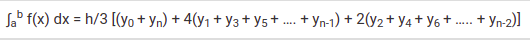We can get a quick approximation for definite integrals when we divide a small interval [a, b] into two parts. Therefore, after dividing the interval, we get;
x0= a, x1= a + b, x2 = b
Hence, we can write the approximation as;
∫ab f(x) dx ≈ S2 = h/3[f(x0) + 4f(x1) + f(x2)]
S2 = h/3 [f(a) + 4 f((a+b)/2) + f(b)]
Where h = (b - a)/2
This is the Simpson's 1/3 rule for integration.

Procedure

  1. Define function f(x)
  2. Enter initial limit (a), final limit (b), interval (i)
  3. Calculate step size (h)
  4. Using for loop calculate:
    for i= 2:2:n
    sum1= sum1+ y(i)
  5. for i= 3:2:n-1
    sum2= sum2+ y(i)
  6. sum= f(a)+f(b)
  7. ans= h/3 * (sum + 4 * sum2 + 2 * sum1)
  8. Display the answer

Python Code

                        
                           
import math
a= int(input("Enter the lower limit: "))
b= int(input("Enter the upper limit: "))
n= int(input("Enter the length: "))

def f(x):
    return math.sqrt(1-x**2)

def simpson13(a,b,n):
    h= (b-a)/n
    sum= f(a)+f(b)

    for i in range(1,n):
        c = a+i*h
        if i%2==0:
            sum+=2*f(c)
        else:
            sum+=4*f(c)

    ans= (h/3)*sum
    return ans

result= simpson13(a,b,n)
print("Result by Trapezoidal method is: ",result)

Observations

Take Observations from the method and tabulate it for the given intervals.

Plot a graph also. (Interval vs Value).

Result

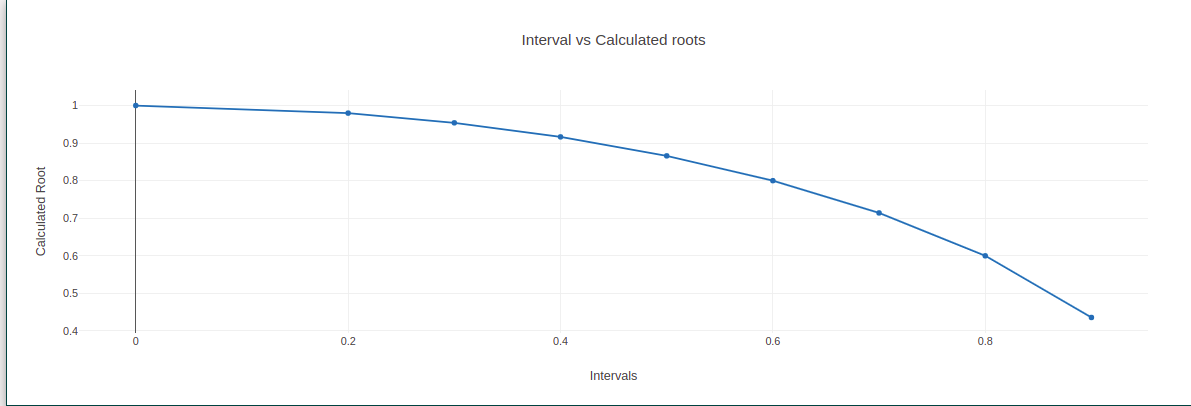
Hence we calculate the definite integral
If the 1/3 rule is applied to n equal subdivisions of the integration range [a, b], one obtains the composite Simpson's rule. Points inside the integration range are given alternating weights 4/3 and 2/3.

References

Simpson 1/3 method Byju's

Simpson 1/3 method Wikipedia